Beginner's Guide

Day and Time

How long is a day? What time is it? To most people these are simple questions with straightforward answers. There are 24 hours in a day, and the time of day can be read off a clock and these days mostly from your cellphone. This is not the case in astronomy where these questions are more complicated. We have Standard Time, Daylight Savings Time, Local time, Local Mean Time, Greenwich Mean Time, Universal Time, and Sidereal Time. Please note though we feel it is good to know what all these are, it's not important that you ever calculate them. We have computers and software to do that task. Incidently, our discussion of days and years is strictly referring to Earth. Days and years also apply to other planets and have their own values, but this is not what we will discuss here.

 

 

Two Units of Time

Fundamentally we have just two units of basic time. We have the rotational period of the Earth as in spins on its axis which we call a day. And we have the period that Earth revolves around the sun which we call a year. Sounds simple enough, but it turns out not to be the case. First of all there is absolutely no direct relationship of the Earth's rotation and revolution periods. For example, we don't have exactly 365 days in a year. The figure is close but not exactly equal to 365.25 days. To make up for this fraction we have a leap year where we add one additional day which is February 29th. Surely the rotational period of the Earth must be simple, right? It really is, but it shouldn't surprise you that we live our lives with the huge influence of the sun and that will complicate things.

 

Solar Time

Though nearly everyone knows the Earth rotates around its axis every day, that is not how we measure a day. We do it by the sun. When the sun crosses the meridian (the north/south) line that is noon, or 12:00PM. But it's not quite that simple.

 

Apparent Solar Time

This is true solar time. It is all based on noon (12:00PM) and when it crosses the meridian. It is sometimes referred to as Sundial Time as this is the time that will be shown on a sundial. You are also using true solar time when you estimate the time of day by looking at the position of the sun.

 

Mean Solar Time

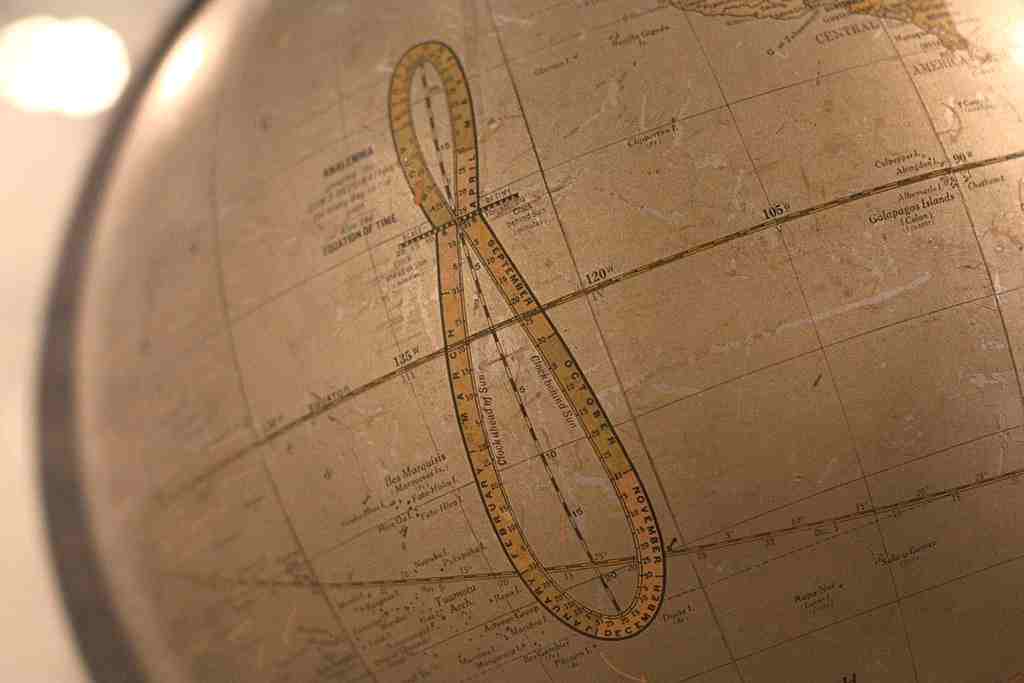
But Apparent Solar Time actually varies a little from day to day. The picture on the right is called the Analemma. All of these images of the sun were taken at the exact same time of day. So you can see that sometimes the sun is behind and sometimes it's ahead. At exactly 4 times a year the sun is exactly in the middle and only on those dates does the sun cross the meridian at noon. Mean Solar Time is simply Apparent Solar Time averaged through an entire year which is exactly 24 hours per day. You'll be seeing the word Mean used again so know that it means Average.

So why does this happen? The Earth's orbit around the sun is not a perfect circle, but an ellipse. The speed of Earth varies with its distance to the sun: faster when it is closer, slower when it is farther.

On most of the older globes, they would display the analemma and always somewhere in the Pacific Ocean. But on a globe it shows the information for the Equation of Time which describes the discrepancy between Apparent Solar Time and Mean Solar Time. During the year the difference between the two can be as much as 16 minutes fast and 14 minutes slow. So the Equation of Time is needed when you're using a sundial for time.

 

Local Mean Time

Local Mean Time (LMT) is Mean Solar Time applied to your location. Sometimes referred to as Local Civil Time, or just mean time or local time. This is the time that is used in astronomy because this time is needed to find the precise location of stars and all other objects other than the sun. For the sun, you need apparent solar time. You can calculate LMT by adding (or subtracting) the difference between your longitude and the meridian of your time zone: 4 minutes per degree. For example, let's take our MAS Observatory in New Berlin where the longitude is W88° 08' 53".89.

1) First convert that to decimal for ease: W88° 08' 53".89 = W88.898°
2) Now subtract the meridian for the Central Time Zone: W90°. 88.898 - 90 = -1.102°
3) Convert to time at 4 minutes per degree. -1.102 X 4 = -4.408 minutes.

So for the MAS Observatory location, you would subtract 4.408 minutes from CST. Please note that you have to subtract an additional hour if it's CDT. But, as we stated earlier, your need to be able to calculate this is almost nil because computers automatically do this within almost all astronomy software. We only think it's important that you know how it's calculated.

 

Standard Time

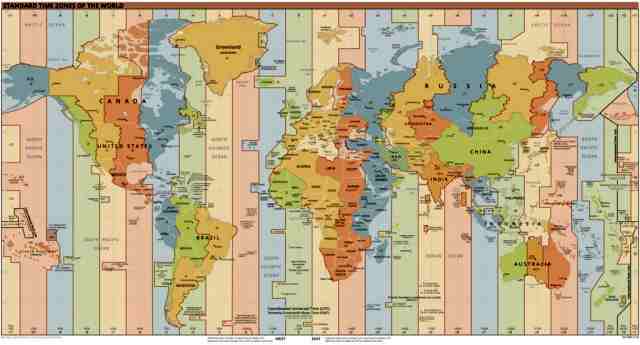Standard Time is what you are most familiar because it's the time we actually use on a day by day basis. We don't use Mean Time because every location would have a different time. Before 1884 this wreaked havoc on train schedules as every city had a different time. This was finally addressed in 1883 when it was decided that Standard Time was necessary and that the world would be divided into 24 time zones, each centered on 15° longitudes, either East or West of the Prime Meridian (Greenwich Mean Time). In Milwaukee we are in the Central Standard Time Zone which means we are 6 hours west of Greenwich Mean Time, so 7 hours if on daylight time (CDT).

Though the time zone map shows a fairly recent version, you should know that individual countries can make the rules within their boundaries and things do change, but generally not dramatically.

 

Greenwich Mean Time

Greenwich Mean Time (GMT) is the Solar Mean Time on the Prime Meridian which by convention goes through the Royal Observatory at Greenwich, London, England. It is Zone 0. Unfortunately, historically, there have been two different conventions for GMT numbering hours. In astronomy the convention (going back to the Greeks) was to number the hours starting at noon and does persist to this day because of Julian Day numbering. But the civil convention started the numbering at midnight and that goes back to the Roman Empire. As of 1925 there is no ambiguity as they standardized GMT as always starting at midnight. But unfortunately in astronomy we go way back in time so this continues to be an issue which has been solved by the introduction of Universal Time.

 

Universal Time

Universal (UT) is the same as GMT. This is the time we prefer in astronomy and it starts at midnight. Utilization of UT solves the ambiquity that can crop up with GMT going back in time.

 

Sidereal Time

Sidereal Time (sometimes referred to as Star Time) is based on the rotation of the Earth. Just like solar time it is divided into 24 hours, but it's about 4 minutes slower. Sidereal Time is a scale based on Earth's rotation as measured relative to the fixed stars. Sidereal Time is needed to point a telescope at the proper coordinates of any celestial object.

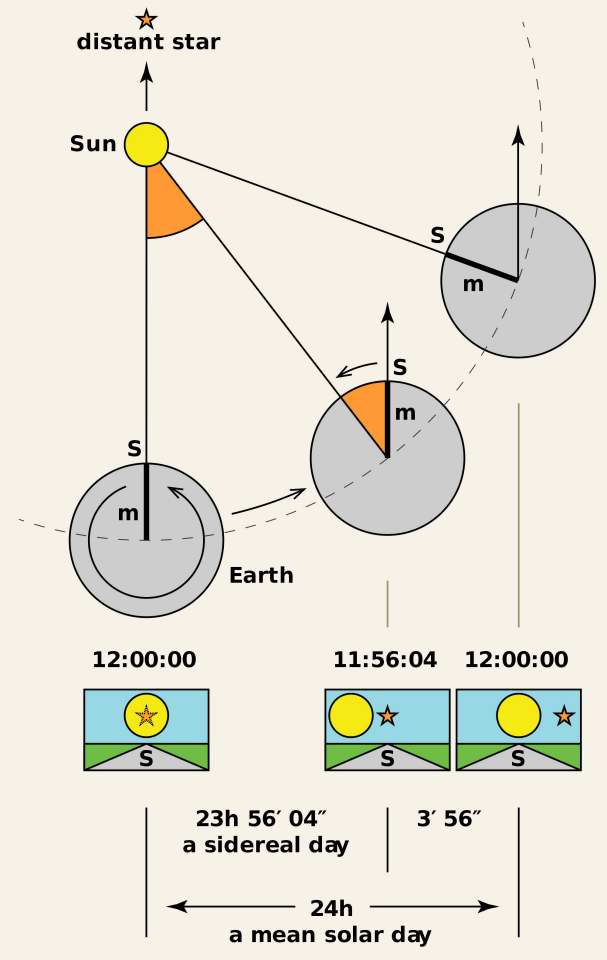
The diagram to the right shows how Sidereal Time differs from Mean Solar Time. You might first think that it rotates in 24 hours, just like the sun returns to the meridian in 24 hours, but the Earth is in orbit so it's position is constantly changing. The Earth is rotating on its own, but because of the orbit it's also rotating from that, although a far smaller amount. The effect is that in 24 hours (Mean Solar), a star will appear to move almost 1 degree further. A Sidereal Day is about 23 hrs 56 min 4.0905 sec. Because the Earth will rotate exactly once more time than its daily rotation, there is exactly more more Sidereal Day than the days in a Solar Year.

 

Year

A Year is the time it takes for Earth to make a full revolution around the sun. It is just that simple. But it does become a little complicated when we attempt to divide a year into days because there is no direct relationship. There are 365.242196 days in a year. Dealing with that fraction is why we either have or don't have leap years. You probably know we have a leap year every 4 years where we add 1 full day. But that would imply that there are 365.25 days per year and the actual number is a little lower than that. What actually happens is that we don't have leap years at the century mark (1700, 1800, 1900, 2000, 2100, ...) unless the year is evenly divisible by 400. If it is (like 2000) then that year is a leap year. By this rule a year would be 365.2425 days. Fairly close, but still a small fraction is left. So every 3000+ years one of the leap years must be excluded. But at this point things get a little dicey because the orbit of Earth is not that consistent. Earth's orbit is effected by Jupiter so the period sometimes slows or speeds up a bit.

 

Julian Day

Time is an extremely important part of astronomy and especially when it comes to analysis. And we've been collecting data for a few thousand years at this point. So an efficient method of recording time is necessary. But our usual system of dates is clumsy and our calendar has changed several times in the past. And then we have the problem of leap years so every year is not the same length so making calculations is especially problematic. For example, how long is it from November 15, 2018 at 2PM until March 30, 2021 at 10PM? This is where the Julian Day comes in where they just keep track of time by counting days.

To make this work you need a baseline and the date chosen was January 1, 4713 BC, starting at noon. This is therefore Julian Date 0.

Let's now address our date problem which is easily solved by converting the dates to Julian Date (JD). Note that these date/times are in Universal Time (UT).

November 15, 2018 (2PM) = JD 2458438.08333
March 30, 2021 (10PM) = JD 2459303.41667
Subtracting, we get 865.33334 days. So, 865 days, 8 hrs, 0 min, 0.576 sec.

Needless to say calculating a Julian Day is challenging. But we have a calculator which can access here to easily do the conversion.

Julian Dates are used almost exclusively in variable star astronomy. And outside of astronomy, it is used in software, although they many times use various base dates.